|
Utilización de Barlow, Reductor Focal y Proyección Ocular
¿CÓMO AJUSTAR LA DISTANCIA FOCAL?
Para alcanzar las distancias focales grandes requeridas en la representación de imagenes del alta resolución, se usan las extensiones focales: Las lentes de Barlow y oculares. Las lentes de Barlow y oculares no son los opositores, ellos son complementarios: el primero se usa para los coeficientes de amplificación moderados , el segundo para los coeficientes de amplificación grandes, por otro lado, en la representación de imagenes de cielo profundo, los reductores focales son útiles para disminuir el tiempo de exposición y aumentar el campo .
Los cálculos de distancia focal resultante son simples, para ello se necesitan sólo una calculadora de y una regla graduada.
Barlow lente de proyección
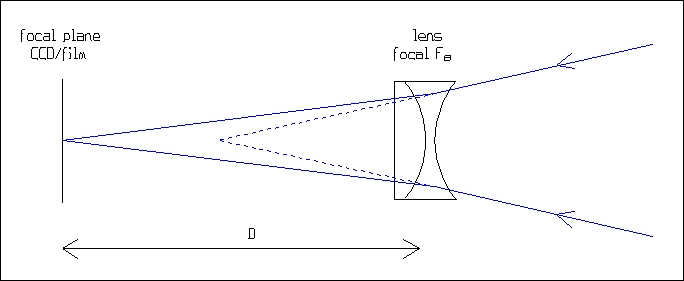
Una lente de Barlow es un grupo de lentes con un poder negativo que amplifica la distancia focal primaria del telescopio. Su coeficiente de amplificación es normalmente escrito en su tubo. Un punto importante es que este factor sólo es verdad para una distancia específica entre la lente y el plano focal . Si esta distancia cambia, cambian los coeficientes de amplificación.
La relación entre el coeficiente de amplificación A, la distancia focal FB de la lente de Barlow y el D de distancia entre la lente y el plano focal es:
A = D/FB + 1
(realmente, la distancia focal de una lente divergente tiene un valor negativo, pero aquí nosotros consideramos su valor absoluto).
ejemplo: una lente de Barlow cuya distancia focal es 100 mm, se instala a una distancia de 150 mm del detector del CCD (o la película). Su coeficiente de amplificación es A = 150/100 + 1 = 2.5x. En un 200 mm F/D 10 telescopio, la último distancia focal es 2000*2.5 = 5000 mm, y la proporción focal final es 10*2.5 = 25.
La fórmula muestra que cuando la distancia aumenta, el coeficiente de amplificación aumenta, y que un Barlow ' 2x ' sólo da un verdadero coeficiente de amplificación de 2 si su distancia del plano focal es igual a su distancia focal (100 mm en el ejemplo anterior). Si esta distancia se dobla, el coeficiente de amplificación se vuelve 3x.
Una vez que la distancia focal resultante del telescopio es escogida, el coeficiente de amplificación debe ajustarse para alcanzar este valor, cambiando la distancia entre la lente de Barlow y el plano focal. La fórmula puede invertirse para obtener el D de A y FB: D = FB (A - 1)
En el ejemplo anterior, si la distancia focal requerida del telescopio es 6200 mm, el coeficiente de amplificación debe ser 6200/2200 = 2.8x. La distancia entre el detector del CCD (o la película) y la lente cuya distancia focal es 76 mm, debe ser el D = 76*(2.8 - 1) = 137 mm.
La mejor manera de usar una lente de Barlow es destornillando la parte de la lente de la parte que recibe el ocular, e insertándolo en un adaptador ocular fotográfico de 42 mm. Aunque estos métodos permiten mover la lente un poco dentro del adaptador, pueden necesitarse algunos anillos de longitudes diferentes para alcanzar la distancia deseada entre la lente y el plano focal.
La calibración de una lente de Barlow
Desgraciadamente, la distancia focal de una lente de Barlow normalmente no se conoce a priori. Por consiguiente, debe determinarse por ejemplo de las imágenes de un objeto conocido, un planeta o un par de estrellas. El método es:
1. tome una imagen de un planeta cuyo diámetro angular P (en segundos de arco) es conocido de las efemérides.
2. Mida el tamaño de la imagen S (en las micrones) en el detector CCD o la película
3. calcule la distancia focal resultante F (en milímetros) con ' la fórmula del ejemplo': F = 206 S/P
4. tome otra imagen del mismo objeto, pero ahora sin la lente de Barlow: la misma fórmula da la distancia focal primaria FP del telescopio.
5. calcule el coeficiente de amplificación de la lente de Barlow: UN = EL F / FP
6. Mida la distancia D (en milímetros) entre la lente y el plano focal
7. calcule la distancia focal FB de la lente de Barlow con la fórmula: FB = D / (A - 1)
Ejemplo: una imagen de Júpiter cuyo tamaño es 46 ", se toma con un KAF-0400 CCD detector (9 pixeles micrones) detrás de una lente de Barlow. El tamaño del planeta es 170 pixeles, mientras correspondiendo a 170*9 = 1530 micrones. La distancia focal resultante del telescopio es el F = 206*1530/46 = 6850 mm. Sin la lente de Barlow, el tamaño de la imagen es 55 pixeles (495 micras), correspondiendo a una distancia focal primaria del telescopio FP = 206*495/46 = 2200 mm. El coeficiente de amplificación es A = 6850/2200 = 3.11x. La distancia entre la lente de Barlow y el detector CCD es 160 mm, entonces la distancia focal de la lente es FB = 130/(3.11 - 1) = 76 mm.
Especialmente con SCTs, medir la distancia focal primaria real del telescopio es una precaución buena, porque esta distancia focal varía según la posición del espejo primario (el espejo secundario cuyo papel es amplificar la distancia focal del espejo primario, se comporta como una lente de Barlow).
La combinación de lentes de Barlow
Debido a los problemas de corrección de aberración, una lente de Barlow no trabaja en las condiciones buenas a cualquier coeficiente de amplificación. Por ejemplo, un lente de Barlow ' 2x ' trabaja correctamente entre 2x y 3x, pero no a las 5x o 6x. Estos coeficientes de amplificación grandes pueden obtenerse con la ayuda de una serie de dos lentes de Barlow de quien se multiplicarán los coeficientes de amplificación.
Los cálculos son:
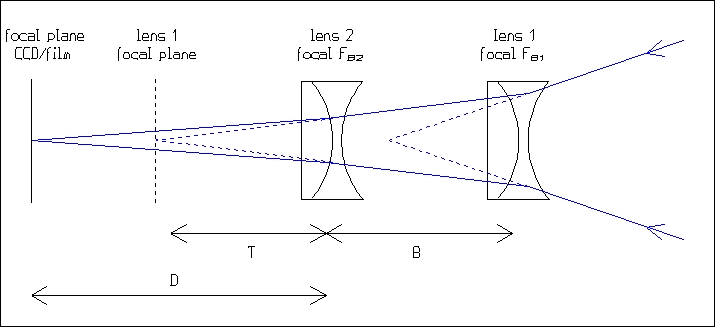
1. dada la distancia focal FB2 de la lente Barlow 2 (la más cerca al plano focal) y su distancia del plano focal D , calcule su coeficiente de amplificación A2
2. la distancia entre la lente 2 y el plano focal que relaciona a la lente 1 es el T = D/A2
3. dado la distancia B entre las dos lentes, la distancia entre la lente 1 y su plano focal es T + B
4. calcule el coeficiente de amplificación A1 de la lente 1 con su distancia focal FB1 y la distancia T + B
5. el coeficiente de amplificación resultante es UN = A1 * A2
El ejemplo: dos lentes de Barlow idénticas cuya distancia focal es 76 mm, están separadas por una distancia de 50 mm. La distancia entre la lente 2 y el detector CCD es 100 mm. Su coeficiente de amplificación es A2 = 100/76 + 1 = 2.3x. La distancia entre la lente 2 y el plano focal que relaciona a la lente 1 es 100/2.3 = 43 mm. La distancia entre la lente 1 y su plano focal es 43 + 50 = 93 mm. El coeficiente de amplificación de la lente 1 es A1 = 93/76 + 1 = 2.2x. El último coeficiente de amplificación A de la combinación de lentes es A = 2.3*2.2 = 5.1x.
La proyección ocular
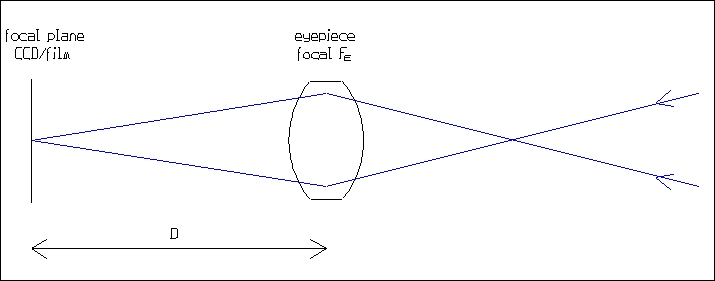
Un ocular visual normal se diseña para dar los rayos paralelos. Pero cuando se usa en fotografía o proyección CCD, da una haz convergente. Por consiguiente, debido a los problemas de corrección de aberraciones (especialmente la curvatura del campo), correctamente sólo funciona a los coeficientes de amplificación grandes, típicamente 6x o más.
La relación entre la distancia focal FE del ocular, el coeficiente de amplificación A y la distancia D entre el ocular y el plano focal es:
A = D/FE - 1
El ejemplo: un ocular de 20 mm, instalado a 180 mm del plano focal, da un coeficiente de amplificación de A = 180/20 - 1 = 8x.
El reductor focal
Un reductor focal es un grupo de lentes con un poder positivo que disminuye la distancia focal primaria del telescopio. Como en el caso de una lente de Barlow, su factor de reducción depende de su distancia focal y su distancia del plano focal. Cuando esta distancia aumenta, la reducción es más pronunciada. Debido a los problemas de corrección de aberración, se aconseja para usar un reductor focal muy cerrado un factor de reducción cerca de su factor nominal.
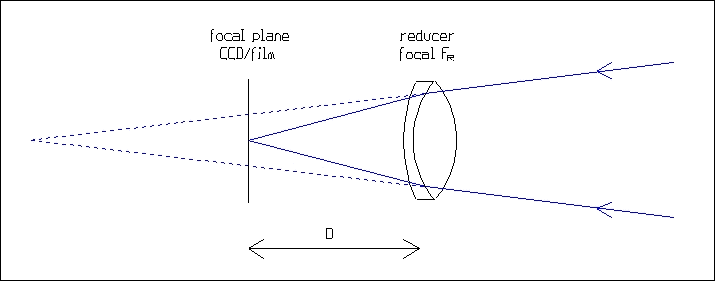
La relación entre el factor de reducción R, la distancia focal FR del reductor y la distancia D entre la lente y el plano focal es:
R = 1 - D/FR
Determinar la distancia focal de un reductor focal es fácil: apunte el Sol (o la Luna) con el reductor solo, y mida la distancia entre la lente y la imagen solar (o lunar).
El reductor de F/6.3 de Meade/Celestron tiene una distancia focal de aproximadamente 230 mm. Por consiguiente, la distancia nominal entre la lente y el plano focal está sobre D = FR*(1 - R) = 230*(1 - 0.63) = 85 mm. sólo está a esta distancia el factor de reducción de este reductor que es un factor de reducción nominal de 0.63x.
El dibujo muestras que un reductor focal mueve el plano focal más cerca del telescopio. En algunos instrumentos, el rango de convergencia no puede ser suficiente para alcanzar el punto con un reductor focal. Además, especialmente en SCTs, los problemas del viñeteo son normalmente más críticos con un reductor que sin uno.
|